top of page

算数を学ぶ時に数字だけでなく、図形を学びます。数字は足し算、引き算、かけ算とわり算を学びますが、図形は三角形や四角形と円を学びましょう。
三角形は「3つの角がある図形」、四角形は「4つの角がある図形」です。角の数だけでなく、辺の数もそれぞれ3つ、4つとなっていて、角の数と辺の数はいっしょです。

くり返しますが、三角形には「角も辺も3つずつ」あります。
次に三角形の面積を考えてみます。三角形の面積は
[ 底辺 × 高さ ÷ 2 = 三角形の面積 ]

なぜ[ 底辺 × 高さ ÷ 2 = 三角形の面積 ]で[÷ 2 ]をするのでしょうか?以下の図を見てみると「赤枠の長方形BEFCを半分にする」と三角形ABCの面積になります。

三角形ABCの3辺はどんな長さでもOKなのではなく、条件があります。

三角形は3つの角度を足すと180°になります。それを図形で説明すると↓になります。
同じ三角形を3つ回転させて並べると、角A + 角B + 角C = 180° になります。

どんな三角形でも同じものを3つ用意すれば、3つの角度の和が180°になります。
三角形にはいろいろ特徴のある三角形があります。
まず、3つの辺が同じ長さ、3つの角が同じ大きさとなる三角形です。
3つの角度は180 ÷ 3 = 60° です。

他には二等辺三角形があります。「二等辺」とは「2つの辺が同じ」という意味なので「2つの辺が同じ三角形」が二等辺三角形です。
2つの辺が同じ長さ、2つの角が同じ大きさとなります。

直角三角形も覚えておきましょう。3つの角のうち、1つが90°です。「直角」は90°という意味ですので「直角のある三角形」ということです。
三角形の角は3つで180°で、そのうち1つが直角90°の場合、残り2つの角を足すと 90°になります(180 - 90 = 90 °)。


さらに直角三角形でもあり、同時に二等辺三角形も覚えておきましょう。1つの角が90°で、2つの辺と2つの角が同じです。
三角形の角は3つで180°で、そのうち1つが直角90°、かつ残り2つの角は同じ大きさということは2つの角はそれぞれ45°です。


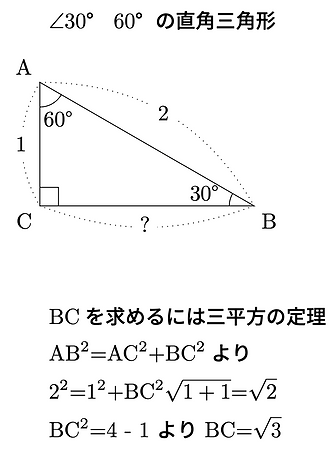
最後に直角三角形でのこりの2つ角が30°, 60°の場合は長辺が短辺の2倍の長さになります。
この直角三角形の角と辺の関係はは小学生の算数だけでなく、中学受験や中学生高校生の数学でもたくさん使います。


三角形の角は3つで180°ですが、ここで「三角形の外角と内角」の性質に面白いものがあります。

中学の数学で”平方根”を学ぶと直角三角形の”三平方の定理”を使えるようになります。
簡単に言えば「直角三角形の斜辺の二乗 = 残り2辺を2乗した和」です。
↓では直角二等辺三角形を用いてますが、どんな直角三角形でも成り立ちます。

直角二等辺三角けい2つの角が30度と60度の直角三角形の[ 1 : 2 :√3 ]でたくさん使われます。高校数学で”三角関数”という分野があるほど直角と辺の長さはよ〜く出てきます。
三角形の「角の二等分線」はコンパスで作図することで求められます。
二等分線は「2辺からの距離が等しい」ので三角形の二等分線を2回引くと「内接円」が作図できます。
内接円の中心を「内心」と呼びます。


三角形の二等分線を活用して「線分の比」を求めることもできます。↓は頻出です。

三角形の内接円と外接円は理解が紛らわしいですが、外接円は「垂直二等分線」の交点です。

三角形には「重心」もあります。「重心」は頂点と中点を結んだ交点です。
さらに
AG : GD = CG : GF = BG : GE = 2 :1
です。


高校数学になると [ sin θ ] [ cos θ ] [ tan θ ] を扱います。
斜辺の長さ = 1 の直角三角形を用いて定義を↓に記します。

三角形の面積は[ sin θ ] を使うと簡単に求めることができます。

正弦��定理という[ sin θ ] を使うと[ 外接円の大きさ ]を求めることができます。反対に「円の大きさや半径」がわかっていれば、角度や三角形の辺の長さを求めることもできます。
↓では[ 円周角の定理 ]をも活用して[ 角A = 角D ]であることを利用しています。

三角形の3辺の長さがわかっていると[ cos θ ] を求めることができます。[ 余弦定理 ]と呼びます。 辺の長さは[ 三平方の定理 ]がまず浮かびますが、 [ 余弦定理 ]では直角三角形でなくとも成立します。

三角形における [角の二等分線( 青の△ ) ]は↓のように[ AB : BC = AD : DC ]の性質があります。証明には「平行の角」と「二等辺三角形」を使っています。

「チェバの定理」は線分の比率と面積の比率で重要な定理です。


「チェバの定理」と並び「メネラウスの定理」も三角形にまつわる比ですが、こちらは「平行な線分」を基に導出されています。
内接円と直角三角形は↓のようになります。

bottom of page
