top of page

合同(記号: ≡)と相似(記号:∽)は似ているけど違います。
合同(記号: ≡)は同じ形、かつ同じ大きさ
相似(記号:∽)は同じ形、でも大きさは違う
合同(記号: ≡)を考えるための条件、まずは「三角形の合同条件」を考えます。
条件は下記の3つです。
-
3つの辺が等しい
-
2辺とはさまれた角が等しい
-
1辺と両端の角が等しい



合同(記号: ≡)を角の二等分線でも作図できます。

合同(記号: ≡)「四角形の合同条件」を考えます。
正方形なら「一辺の長さが等しい」

「直角に交わり対角線の長さが等しい」→ 合同なひし形です。

とある一点から円の接線を引くと、点と円の中心を結ぶ線は接線が作る角の二等分線です。

内接円と3組の接線の関係も使われます。

次にまずは「三角形の相似」を考えます。
相似を考える時に
-
2つの角が等しい
-
3組の辺の長さについて比が等しい
-
2組の辺の長さについて比とはさまれた角が等しい
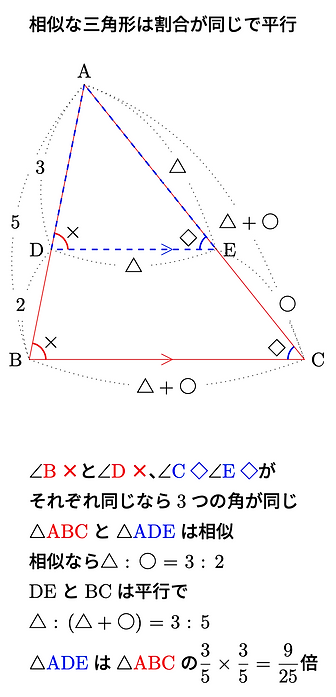
また「相似の面積比」は2乗の比になります。つまり、辺の長さが2倍なら面積は2×2の4倍、辺の長さが3倍なら面積は3×3の9倍です。
「相似な図形の面積比」を直角三角形に活用すると「三平方の定理」を証明できます。

正方形をはじめ、四角形の場合も「相似の場合、面積比は2乗の比」です。
↓正方形の1辺が「2:1の長さ比ならば、面積比は2×2=4より4:1」です。

平面について「相似の場合、面積比は2乗の比」ですが、相似の体積については「相似の場合、体積比は3乗の比」です。
↓立方体の1辺が「2:1の長さ比ならば、体積比は2×2×2=8より8:1」です。

円の中で「2辺が交差する時には相似な三角形」ができます。 円周角の定理により角が等しいからです。
相似な図形の比より「方べきの定理」が成り立ちます。

こちらも「方べきの定理」です。接線の角度についての知識も問われます。


円錐の中に球がある問題は三角形の相似、円の相似の両方があります。
bottom of page

