top of page

三角関数といえば「サイン、コサイン、タンジェント」と”数学を勉強してなんの意味があるの?”のやり玉に挙がることがあります(他には微分積分についても似た意見が指摘されます。
意外に思うかもしれませんが流行の「データサイエンス」 で[ cos θ ]をよく使います。ネットショッピングのおすすめ商品が表示される機能にも三角関数(+ベクトル)が活用されています。
三角関数は図形や微分積分、ベクトルや複素数など他の分野にまたがった問題が頻出で す。
まずは[ sin θ, cos θ, tan θ]の基本から2倍角や半角、[ 角α + 角β ]など角の足し算引き算を理解し使いこなせるようになることが大切です。

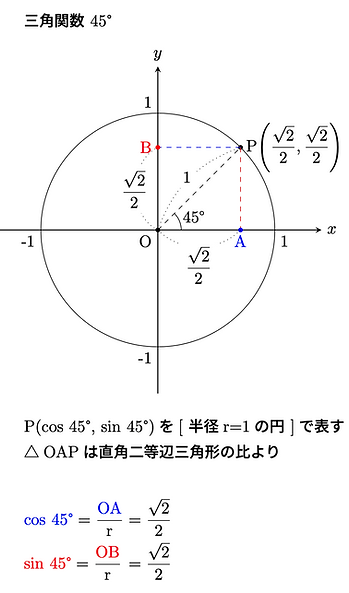
↑の図では半径1の円でしたが、[ 半径 = r ]と一般的な三角関数にすると↓のとおりです。
rは[ radius ]の頭文字です。

三角関数の基本で大事なのが
360° = 2π
180° = π
です。
一周が[ 2π ] なので三角関数[ θ ] の角は
θ = θ + 2nπ ( nは整数 )
と表したりします。

直角三角形の代表例から 30°、45°、60° といった角度のsinやcosをあてはめられます。


三角関数のグラフは「波型」です。円は2πで一周ですので[ sinθ ] [ cosθ ]は2πで周期性があります。

sinやcosの次はtanです。分子分母はsinやcosです。

tanはcosが分母にありますので[ 分母を1 ]にすれば↓のように表すことができます。

三平方の定理や円の方程式と同じように
sinやcosの二乗を足すと1です。角の大きさに関係なく成り立ち、受験数学でとてもよく使います。

三角関数の応用について
sin (α + β)
cos (α + β)
について [ α ] [ β ] については↓のように三角形の相似を利用して作図することができます。
式の暗記もありですが、作図すると理解しやすいです。
[ OQ = cos β ] と [ △OQR と △QPT が相似 ] がポイントです↓。


三角関数[ α ] [ β ]が同じ大きさだった場合、α = βなので 2α となり2倍角の公式が導出されます。
特にcos 2αは三角関数の後、微分積分などでも使う公式です。

cos 2αは三角関数は↓のような変形もよく使います。


2倍角をグラフにすると[ 周期が半分 ]になることがわかります(↓の赤線)。3倍でもn倍でも考え方は一緒です。

三角関数はx軸やy軸に対称となります。sinとcosの符号がどのように変わるか、どのように角度をとるかややこしい部分があります。
↓では[ θ ]と[ 60° ]と文字、数字を用いて対称な三角関数を説明しております。



三角関数の対称性を[ + ] を [ − ]に置き換えると
sin[ α + β ] → sin[ α − β ]
cos[ α + β ] → cos[ α − β ]
を導くことができます。

三角関数 sin[ α + β ]と cos[ α + β ] を用いてtan[ α + β ]を式変形で導出します。


tan[ α − β ]については、「関数の2直線のなす角」と関係してきます。

三角関数の加法定理を反対にすることで↓を導出することができます。積分の際に式変形で活用します。

2倍角の三角�関数を応用して[ 半角の三角関数 ]を導出することができます。2乗の乗数が減るのもポイントです。
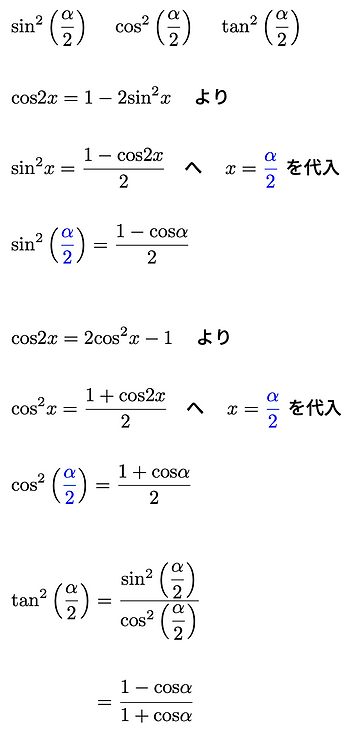
三角関数の加法定理を反対向きに計算すると「三角関数の合成」ができます。式変形に慣れることが大事で、三角関数の微分積分でも活用されます。
sinθ+ cosθ を[ sin か cos のどちらか ] に統一できる(=合成)公式です。
図にするとややこしいのですが一応↓このような形です。[ sinθ はy軸 ]、[ cosθ はx軸 ]に表されるのを[ sin か cos のどちらか ] に寄せています(↓はsin に寄せた例です)。
-
a と b から sinα, cosα を算出
-
三角関数の加法定理
(a と b をsin or cos のどっちにするの?と慣れないうちは難しいかもしれませんが、加法定理の式変形にあてはまるように設定するのがポイントです←要は変形したい式に合うようにa と bを置くのが大事)

sinθ+ cosθをcos(cos(α-β))へ導出できます。[ a と b } の置き方を反対にしています。

sinθ+ cosθをcos(cos(α-β))へ導出すると、「ベクトルの内積=cos(cos(α-β))の三角関数の合成」を意味にしていることがわかります。
三角関数とベクトルがつながるのが不思議ですが数学的にはこうなります。

cosについても「三角関数の合成」ができます。
-
a と b から sinα, cosα を算出
-
三角関数の加法定理

「三角関数の微分」は不思議ながら↓のようになります。

bottom of page
